Πώς υπολογίζετε το RSA σας;
Πώς υπολογίζετε το RSA σας;

Πίνακας περιεχομένων:

Anonim

Ένα πολύ απλό παράδειγμα κρυπτογράφησης RSA

  1. Επιλέξτε πρώτους p=11, q=3.
  2. n = pq = 11,3 = 33. phi = (p-1) (q-1) = 10,2 = 20.
  3. Επιλέξτε e=3. Ελέγξτε gcd(e, p-1) = gcd(3, 10) = 1 (δηλαδή οι 3 και 10 δεν έχουν κοινούς παράγοντες εκτός από 1),
  4. Υπολογίστε το d έτσι ώστε ed ≡ 1 (mod phi) δηλ. υπολογίστε d = (1/e) mod phi = (1/3) mod 20.
  5. Δημόσιο κλειδί = (n, e) = (33, 3)

Λαμβάνοντας υπόψη αυτό, πώς λύνετε το RSA;

  1. Βήμα-1: Επιλέξτε δύο πρώτους αριθμούς και. Ας πάρουμε και.
  2. Βήμα-2: Υπολογίστε την τιμή του και. Δίνεται ως, και.
  3. Βήμα-3: Βρείτε την τιμή του (δημόσιου κλειδιού) Επιλέξτε, έτσι ώστε να είναι συμπληρωματική.
  4. Βήμα-4: Υπολογίστε την τιμή του (ιδιωτικού κλειδιού) Η συνθήκη δίνεται ως:
  5. Βήμα-5: Κάντε την κρυπτογράφηση και την αποκρυπτογράφηση. Η κρυπτογράφηση δίνεται ως,

Επίσης, γνωρίζετε, τι είναι το δημόσιο κλειδί στο RSA; RSA αλγόριθμος. Είναι ένας ασύμμετρος κρυπτογραφικός αλγόριθμος. Ασύμμετρη σημαίνει ότι υπάρχουν δύο διαφορετικά κλειδιά . Αυτό ονομάζεται επίσης δημόσιο κλειδί κρυπτογραφία, γιατί ένα από τα κλειδιά μπορεί να δοθεί σε οποιονδήποτε. Το άλλο κλειδί πρέπει να διατηρηθεί ιδιωτικός.

Λαμβάνοντας υπόψη αυτό, τι είναι ο αλγόριθμος RSA με παράδειγμα;

Αλγόριθμος RSA είναι η ασύμμετρη κρυπτογραφία αλγόριθμος . Όπως το όνομα περιγράφει ότι το Δημόσιο Κλειδί δίνεται σε όλους και το Ιδιωτικό κλειδί παραμένει ιδιωτικό. Ενα παράδειγμα ασύμμετρης κρυπτογραφίας: Ένας πελάτης (για παράδειγμα browser) στέλνει το δημόσιο κλειδί του στον διακομιστή και ζητά ορισμένα δεδομένα.

Τι σημαίνει RSA;

Μια τεχνολογία κρυπτογράφησης δημόσιου κλειδιού που αναπτύχθηκε από RSA Data Security, Inc. Το ακρωνύμιο περίπτερα για τους Rivest, Shamir και Adelman, τους εφευρέτες της τεχνικής. ο RSA Ο αλγόριθμος βασίζεται στο γεγονός ότι δεν υπάρχει αποτελεσματικός τρόπος να συνυπολογίσουμε πολύ μεγάλους αριθμούς.

Συνιστάται:

Πώς υπολογίζετε τον χρόνο υπηρεσίας στην Προσομοίωση;

Πώς υπολογίζετε τον χρόνο υπηρεσίας στην Προσομοίωση;

Χρόνος υπηρεσίας (λεπτά) = συνολικός χρόνος εξυπηρέτησης (λεπτά) συνολικός αριθμός πελατών = 317 100 = 3,17 λεπτά Μέσος χρόνος ενδιάμεσης άφιξης (λεπτά) = άθροισμα των χρόνων μεταξύ των αφίξεων (λεπτά) αριθμός αφίξεων &μείον; 1 = 415 99 = 4,19 N.B.E[χρόνος ενδιάμεσης άφιξης] = 1+8 2 = 3,2 λεπτά

Πώς υπολογίζετε τη διακύμανση σε έναν συγκεντρωτικό πίνακα;

Πώς υπολογίζετε τη διακύμανση σε έναν συγκεντρωτικό πίνακα;

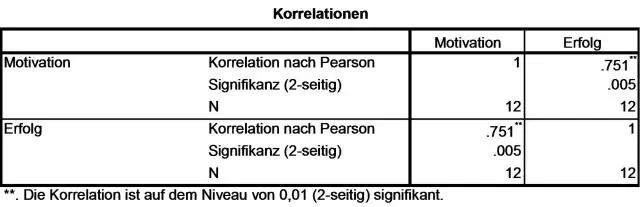
Δημιουργήστε μια προβολή διακύμανσης συγκεντρωτικού πίνακα μήνα σε μήνα για την αναφορά σας στο Excel Κάντε δεξί κλικ σε οποιαδήποτε τιμή εντός του πεδίου προορισμού. Επιλέξτε Ρυθμίσεις πεδίου τιμών. Κάντε κλικ στην καρτέλα Εμφάνιση τιμών ως. Επιλέξτε % διαφορά από την αναπτυσσόμενη λίστα

Πώς υπολογίζετε το χαμηλότερο φράχτη;

Πώς υπολογίζετε το χαμηλότερο φράχτη;

Οι φράχτες βρίσκονται συνήθως με τους ακόλουθους τύπους: Επάνω φράχτη = Q3 + (1,5 * IQR) Κάτω φράχτη = Q1 – (1,5 * IQR)

Πώς αλλάζετε τον κωδικό πρόσβασής σας στο iPhone σας από τον υπολογιστή σας;

Πώς αλλάζετε τον κωδικό πρόσβασής σας στο iPhone σας από τον υπολογιστή σας;

Πατήστε Ρυθμίσεις > [το όνομά σας] > Κωδικός πρόσβασης και ασφάλεια. Πατήστε Αλλαγή κωδικού πρόσβασης. Εισαγάγετε τον τρέχοντα κωδικό πρόσβασης ή τον κωδικό πρόσβασης της συσκευής σας, μετά πληκτρολογήστε έναν νέο κωδικό πρόσβασης και επιβεβαιώστε τον νέο κωδικό πρόσβασης. Πατήστε Αλλαγή ή Αλλαγή κωδικού πρόσβασης

Πώς συνδέετε τις επαφές σας στο Facebook με το τηλέφωνό σας;

Πώς συνδέετε τις επαφές σας στο Facebook με το τηλέφωνό σας;

Για να ανεβάσετε τις επαφές του κινητού σας τηλεφώνου στο Facebook: Από την εφαρμογή Facebook για iPhone ή Android, πατήστε. Πατήστε Φίλοι. Πατήστε Μεταφόρτωση επαφών στο κάτω banner και μετά πατήστε Έναρξη. Από τις συνομιλίες, πατήστε την εικόνα του προφίλ σας στην επάνω αριστερή γωνία. Πατήστε Άτομα. Πατήστε Μεταφόρτωση επαφών για να ενεργοποιήσετε ή να απενεργοποιήσετε αυτήν τη ρύθμιση