Βίντεο: Ποιο γράφημα χρησιμοποιείται για την προβολή των μονομεταβλητών ακραίων τιμών;
2024 Συγγραφέας: Lynn Donovan | [email protected]. Τελευταία τροποποίηση: 2023-12-15 23:45
1. Μονομεταβλητή μέθοδος. Μία από τις απλούστερες μεθόδους ανίχνευσης ακραίες τιμές είναι το χρήση των οικοπέδων κουτιού. Ενα κουτί οικόπεδο είναι ένα γραφικό απεικόνιση για την περιγραφή της κατανομής των δεδομένων. Οικόπεδα κουτιού χρήση το διάμεσο και το κάτω και άνω τεταρτημόριο.
Με αυτόν τον τρόπο, τι είναι ένα μονομεταβλητό γράφημα;
Μονομεταβλητή Δεδομένα και Διμεταβλητά Δεδομένα. Για παράδειγμα, αν καταγράψω τις ηλικίες όλων των μαθητών σε ένα σχολείο και γραφική παράσταση τα δεδομένα μου, τότε θα υπήρχε μόνο μία μεταβλητή, η ηλικία των μαθητών. Αυτός ο τύπος δεδομένων είναι γνωστός ως μονομεταβλητή δεδομένα και δεν ασχολείται με σχέσεις, αλλά μάλλον χρησιμοποιείται για να περιγράψει κάτι.
Ομοίως, πώς αναλύετε τις ακραίες τιμές; Ενα ακραία είναι οποιοδήποτε σημείο δεδομένων που είναι σαφώς διαφορετικό από τα υπόλοιπα σημεία δεδομένων σας.
- Περιορίστε τα ακραία δεδομένα σας. Ένας άλλος τρόπος για να χειριστείτε τις πραγματικές ακραίες τιμές είναι να τις καλύψετε.
- Εκχωρήστε μια νέα τιμή. Εάν μια ακραία τιμή φαίνεται να οφείλεται σε λάθος στα δεδομένα σας, δοκιμάστε να υπολογίσετε μια τιμή.
- Δοκιμάστε μια μεταμόρφωση.
Γνωρίζετε επίσης, ποιος είναι ο συνηθισμένος τρόπος εμφάνισης μονομεταβλητών δεδομένων;
ο κοινός τρόπος εμφάνισης μονομεταβλητών δεδομένων είναι μορφή σε πίνακα. Ο κύριος στόχος είναι η αναπαράσταση του δεδομένα σε ένα τρόπος έτσι ώστε να βρούμε μοτίβα. Υπάρχουν πολλές επιλογές για περιγραφή μονομεταβλητά δεδομένα όπως διαγράμματα ράβδων, ιστογράμματα, διαγράμματα πίτας, πολύγωνα συχνότητας και πίνακες κατανομής συχνότητας.
Πώς αναγνωρίζετε ένα ακραίο σημείο σε μια γραφική παράσταση διασποράς;
Αν ένα σημείο του α διάγραμμα διασποράς είναι πιο μακριά από τη γραμμή παλινδρόμησης από κάποιο άλλο σημείο, τότε το διάγραμμα διασποράς έχει τουλάχιστον ένα ακραία . Εάν ένας αριθμός σημείων είναι η ίδια πιο απομακρυσμένη από τη γραμμή παλινδρόμησης, τότε όλα αυτά τα σημεία είναι ακραίες τιμές.
Συνιστάται:
Ποιο είναι το ερώτημα που χρησιμοποιείται για την εμφάνιση όλων των ονομάτων πινάκων στον SQL Server;
Υπάρχουν δύο τρόποι για να βρείτε όλα τα ονόματα των πινάκων, ο πρώτος είναι χρησιμοποιώντας τη λέξη-κλειδί "SHOW" και ο δεύτερος είναι με ερώτημα INFORMATION_SCHEMA
Ποιο πρότυπο ασφαλείας ορίζει το NIST SP 800 53 για την προστασία των ομοσπονδιακών συστημάτων των ΗΠΑ;
Το NIST Special Publication 800-53 παρέχει έναν κατάλογο ελέγχων ασφάλειας και απορρήτου για όλα τα ομοσπονδιακά συστήματα πληροφοριών των ΗΠΑ εκτός από αυτά που σχετίζονται με την εθνική ασφάλεια. Δημοσιεύεται από το Εθνικό Ινστιτούτο Προτύπων και Τεχνολογίας, το οποίο είναι μια μη ρυθμιστική υπηρεσία του Υπουργείου Εμπορίου των Ηνωμένων Πολιτειών
Ποιο κλειδί χρησιμοποιείται για την κρυπτογράφηση και την αποκρυπτογράφηση μηνυμάτων;
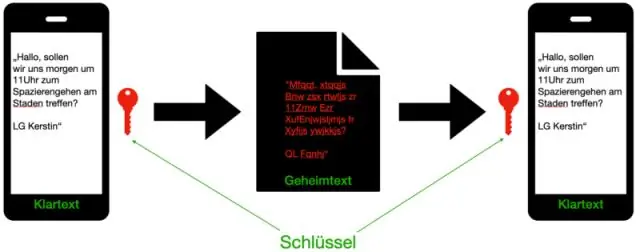
Η ασύμμετρη κρυπτογραφία, γνωστή και ως κρυπτογραφία δημόσιου κλειδιού, χρησιμοποιεί δημόσια και ιδιωτικά κλειδιά για την κρυπτογράφηση και την αποκρυπτογράφηση δεδομένων. Τα πλήκτρα είναι απλά μεγάλοι αριθμοί που έχουν συνδυαστεί αλλά δεν είναι πανομοιότυποι (ασύμμετροι). Ένα κλειδί στο ζεύγος μπορεί να μοιραστεί με όλους. ονομάζεται δημόσιο κλειδί
Τι χρησιμοποιείται για την εκτέλεση όλων των λειτουργιών εισόδου και εξόδου Java;
Επεξήγηση: Το AWT σημαίνει Abstract Window Toolkit, χρησιμοποιείται από μικροεφαρμογές για αλληλεπίδραση με τον χρήστη. 2. Ποιο από αυτά χρησιμοποιείται για την εκτέλεση όλων των λειτουργιών εισόδου και εξόδου στην Java; Επεξήγηση: Όπως σε κάθε άλλη γλώσσα, οι ροές χρησιμοποιούνται για λειτουργίες εισόδου και εξόδου
Ποιο πρωτόκολλο ή υπηρεσία χρησιμοποιείται για τον αυτόματο συγχρονισμό των ρολογιών λογισμικού στους δρομολογητές Cisco;
NTP Ομοίως, μπορεί κανείς να αναρωτηθεί, τι παρέχει το πρωτόκολλο Tacacs+ σε μια ανάπτυξη AAA; TACACS+ υποστηρίζει τον διαχωρισμό των διαδικασιών ελέγχου ταυτότητας και εξουσιοδότησης, ενώ το RADIUS συνδυάζει τον έλεγχο ταυτότητας και την εξουσιοδότηση ως μία διαδικασία.