
- Συγγραφέας Lynn Donovan [email protected].
- Public 2023-12-15 23:45.
- Τελευταία τροποποίηση 2025-01-22 17:22.
ο τετράγωνο έχει τις εξής ιδιότητες:
Ισχύουν όλες οι ιδιότητες ενός ρόμβου (αυτές που έχουν σημασία εδώ είναι οι παράλληλες πλευρές, διαγώνιους είναι κάθετες διχοτόμοι ο ένας του άλλου, και διαγώνιους διχοτομούν το γωνίες ). Ισχύουν όλες οι ιδιότητες ενός ορθογωνίου (η μόνη που έχει σημασία εδώ είναι διαγώνιους είναι συνεπείς).
Από εδώ, οι διαγώνιες ενός ορθογωνίου γωνίας είναι διχοτόμοι;
ο διαγώνιες ενός ορθογωνίου θα διχοτομήσει μόνο το γωνίες εάν οι πλευρές που συναντώνται στο γωνία είναι ίσα: με άλλα λόγια, μόνο αν το ορθογώνιο παραλληλόγραμμο είναι ένα τετράγωνο. Ένας άλλος τρόπος να το σκεφτείς: το γωνία είναι δικαίωμα- γωνία , και το διχοτόμος γωνίας πρέπει να βγει στα μισά δεξιά- γωνία στα πλάγια. Εξ ου και το ορθογώνιο παραλληλόγραμμο πρέπει να είναι τετράγωνο.
Μπορεί επίσης να ρωτήσει κανείς, η διαγώνιος του τετραγώνου διχοτομείται μεταξύ τους; ΕΝΑ τετράγωνο είναι μια ειδική περίπτωση ισοσκελούς τραπεζοειδούς, χαρταετού, παραλληλογράμμου, τετράπλευρου, ορθογωνίου, ρόμβου και τραπεζοειδούς. ο διαγώνιους του α τετράγωνο διχοτόμο ένας αλλο και είναι κάθετοι (που φαίνεται με κόκκινο χρώμα στο παραπάνω σχήμα). Επιπλέον, αυτοί διχοτομήστε το καθένα ζεύγος αντίθετων γωνιών (απεικονίζεται με μπλε χρώμα).
Λαμβάνοντας υπόψη αυτό, σε ποια Τετράπλευρα οι διαγώνιοι διχοτομούν τις γωνίες;
ΕΝΑ τετράπλευρο είναι ρόμβος αν: είναι παραλληλόγραμμο, και ζεύγος γειτονικών πλευρών είναι ίσος, του οι διαγώνιοι διχοτομούνται ο ένας τον άλλον στα δεξιά γωνίες , του οι διαγώνιοι διχοτομούνται κάθε κορυφή γωνία.
Ποια είναι η διαγώνιος του τετραγώνου;
Διαγώνιες του α τετράγωνο . ΕΝΑ τετράγωνο έχει δύο διαγώνιους , τα οποία είναι ευθύγραμμα τμήματα που συνδέουν απέναντι κορυφές (γωνίες) του τετράγωνο . Με άλλα λόγια, το σημείο όπου το διαγώνιους τέμνει (σταυρώνει), χωρίζει το καθένα διαγώνιος σε δύο ίσα μέρη. Καθε διαγώνιος χωρίζει το τετράγωνο σε δύο ίσα ισοσκελή ορθογώνια τρίγωνα.
Συνιστάται:
Τι είναι μια λήψη κάμερας ευρείας γωνίας;
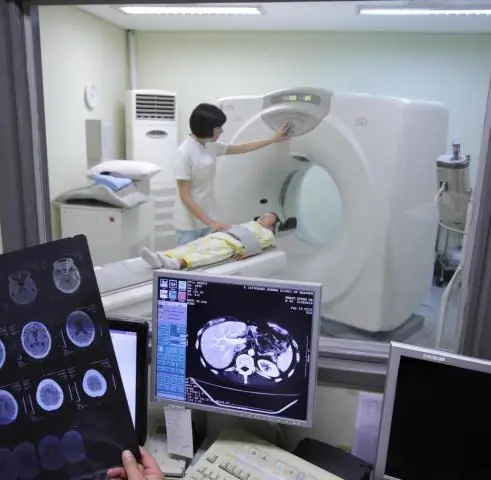
Μια ευρεία λήψη (WS), που αναφέρεται επίσης ως μακρινό στιγμιότυπο, είναι μια γωνία κάμερας που δείχνει ολόκληρο το άτομο που αντιτίθεται και τη σχέση του με αυτό που το περιβάλλει
Ποια είναι η διαφορά μεταξύ μιας μονομερούς σχέσης μιας δυαδικής σχέσης και μιας τριμερούς σχέσης;

Μοναδική σχέση είναι όταν και οι δύο συμμετέχοντες στη σχέση είναι η ίδια οντότητα. Για παράδειγμα: Τα θέματα μπορεί να είναι προαπαιτούμενα για άλλα μαθήματα. Τριαδική σχέση είναι όταν τρεις οντότητες συμμετέχουν στη σχέση
Ποια είναι η διαφορά μεταξύ μιας πλοκής κουτιού και μουστάκι και μιας πλοκής κουτιού;
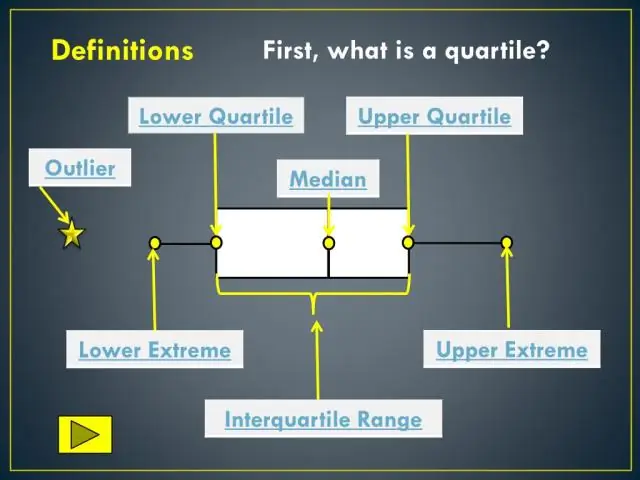
Μια γραφική παράσταση κουτιού και μουστάκι (μερικές φορές ονομάζεται γραφική παράσταση κουτιού) είναι ένα γράφημα που παρουσιάζει πληροφορίες από μια σύνοψη πέντε αριθμών. Σε διάγραμμα κουτιού και μουστάκι: τα άκρα του κιβωτίου είναι τα άνω και κάτω τεταρτημόρια, επομένως το κουτί εκτείνεται στο εύρος των διατεταρτημορίων. η διάμεσος σημειώνεται με μια κάθετη γραμμή μέσα στο πλαίσιο
Ποια είναι η διαφορά μεταξύ μιας ομάδας ασφαλείας και μιας ομάδας διανομής;

Ομάδες ασφαλείας-Ομάδες που χρησιμοποιούνται για την εξασφάλιση της πρόσβασης σε πόρους δικτύου μέσω αδειών. Μπορούν επίσης να χρησιμοποιηθούν για τη διανομή μηνυμάτων email. Ομάδες διανομής-Ομάδες που μπορούν να χρησιμοποιηθούν μόνο για τη διανομή email. έχουν μια σταθερή συνδρομή που δεν μπορεί να χρησιμοποιηθεί για πρόσβαση σε πόρους δικτύου
Ποια είναι η κύρια διαφορά μεταξύ μιας κανονικής ένεσης SQL και μιας τυφλής ευπάθειας ένεσης SQL;

Η Blind SQL injection είναι σχεδόν πανομοιότυπη με την κανονική SQL Injection, με τη μόνη διαφορά να είναι ο τρόπος ανάκτησης των δεδομένων από τη βάση δεδομένων. Όταν η βάση δεδομένων δεν εξάγει δεδομένα στην ιστοσελίδα, ένας εισβολέας αναγκάζεται να κλέψει δεδομένα θέτοντας στη βάση δεδομένων μια σειρά από αληθινές ή ψευδείς ερωτήσεις
