
- Συγγραφέας Lynn Donovan donovan@answers-technology.com.
- Public 2023-12-15 23:45.
- Τελευταία τροποποίηση 2025-01-22 17:22.
ΕΝΑ γραμμικός κώδικας ορίζεται συνήθως ως υποχώρος του Fn για κάποιο πεδίο F (καθώς μιλάτε για bit, μπορείτε να πάρετε F=F2={0, 1}). ο κώδικας Το C που δημιουργείται από έναν πίνακα παραγωγής G είναι το εύρος των σειρών του G. Το εύρος ενός συνόλου διανυσμάτων στο Fn είναι ένας υποχώρος του Fn, επομένως το C είναι ένα γραμμικός κώδικας.
Οι άνθρωποι ρωτούν επίσης, τι είναι ένας γραμμικός κώδικας μπλοκ;
Στη θεωρία κωδικοποίησης, α γραμμικός κώδικας είναι μια διόρθωση σφαλμάτων κώδικας για την οποία οποιαδήποτε γραμμικός Ο συνδυασμός κωδικών λέξεων είναι επίσης μια κωδική λέξη. Οι κωδικές λέξεις στο α γραμμικός κωδικός μπλοκ είναι μπλοκ των συμβόλων που κωδικοποιούνται χρησιμοποιώντας περισσότερα σύμβολα από την αρχική τιμή που θα σταλεί.
Επίσης, τι είναι το σύνδρομο στον κώδικα Hamming; Στη θεωρία κωδικοποίησης, Χάμινγκ Το (7, 4) είναι μια γραμμική διόρθωση σφαλμάτων κώδικας που κωδικοποιεί τέσσερα bit δεδομένων σε επτά bit προσθέτοντας τρία bit ισοτιμίας. Είναι μέλος μεγαλύτερης οικογένειας Κωδικοί Hamming , αλλά ο όρος Κωδικός Hamming αναφέρεται συχνά σε αυτό το συγκεκριμένο κώδικας ότι ο Richard W. Χάμινγκ εισήχθη το 1950.
Τότε, ποιες είναι οι ιδιότητες του γραμμικού κώδικα μπλοκ;
2. ΓΡΑΜΜΙΚΟ ΜΠΛΟΚ ΚΩΔΙΚΟΣΣε a (n, k) γραμμικός κωδικός μπλοκ :1ο τμήμα των k bit είναι πάντα πανομοιότυπο με την ακολουθία μηνυμάτων που πρόκειται να μεταδοθεί. Το 2ο τμήμα των (n-k) bit υπολογίζεται από bit μηνύματος σύμφωνα με τον κανόνα κωδικοποίησης και ονομάζεται bit ισοτιμίας.
Τι είναι ο μη δυαδικός κώδικας;
Μη - δυάδικος διόρθωση σφαλμάτων κωδικούς . Κωδικοί για τη διόρθωση μεμονωμένων μικρών σφαλμάτων, και για τη διόρθωση μεμονωμένων μικρών σφαλμάτων και την ανίχνευση διπλών μικρών σφαλμάτων, σε ένα μήνυμα αυθαίρετου μήκους, για έναν αυθαίρετο αριθμό διαφορετικών σημάτων στο κανάλι, προκύπτουν σε αυτό το άρθρο.
Συνιστάται:
Τι είναι γραμμικό και μη γραμμικό στη δομή δεδομένων;

1. Σε μια γραμμική δομή δεδομένων, τα στοιχεία δεδομένων είναι διατεταγμένα σε γραμμική σειρά, όπου κάθε στοιχείο συνδέεται με το προηγούμενο και το επόμενο γειτονικό του. Σε μια μη γραμμική δομή δεδομένων, τα στοιχεία δεδομένων συνδέονται με ιεραρχικό τρόπο. Στη γραμμική δομή δεδομένων, τα στοιχεία δεδομένων μπορούν να διασχιστούν σε μία μόνο εκτέλεση
Πώς μπορώ να εκτελέσω έναν κώδικα σεναρίου groovy στο Visual Studio;
Απλώς προσθέστε τον φάκελο bin του αποσυμπιεσμένου πακέτου Groovy στη μεταβλητή περιβάλλοντος PATH. Εγκαταστήστε την επέκταση Code Runner για τον κώδικα του Visual Studio. Αυτή η επέκταση μπορεί να ληφθεί από το VS marketplace. Εάν γίνει αυτό, τότε μπορείτε τουλάχιστον να εκτελέσετε ήδη το σενάριο groovy
Πώς επικαλύπτετε ένα γραμμικό γράφημα στο Excel;
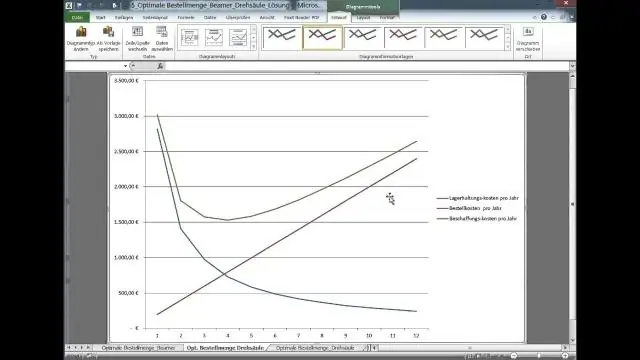
Γράφημα γραμμής επικάλυψης σε γράφημα ράβδων στο Excel Τώρα δημιουργείται ένα γράφημα ράβδων στο φύλλο εργασίας σας, όπως φαίνεται παρακάτω το στιγμιότυπο οθόνης. Στο παράθυρο διαλόγου Αλλαγή Τύπου γραφήματος, επιλέξτεΣυμπλωμένη στήλη – Γραμμή στην ενότητα Συνδυασμός στην καρτέλα Όλα τα γραφήματα και, στη συνέχεια, κάντε κλικ στο κουμπί OK. Επιλέξτε και κάντε δεξί κλικ στη γραμμή που δημιουργήθηκε πρόσφατα και επιλέξτε Μορφοποίηση σειράς δεδομένων στο μενού περιβάλλοντος
Πώς μπορώ να διορθώσω έναν κώδικα Apex στο Salesforce;
Χρησιμοποιήστε σημεία ελέγχου, αρχεία καταγραφής και την καρτέλα Προβολή κατάστασης για να βοηθήσετε στον εντοπισμό σφαλμάτων του κώδικα που έχετε γράψει. Ορίστε σημεία ελέγχου στον κώδικα Apex. Χρησιμοποιήστε τα σημεία ελέγχου της Κονσόλας προγραμματιστή για τον εντοπισμό σφαλμάτων στις κλάσεις και τους κανόνες ετικέτας Apex. Επικάλυψη Apex Code και δηλώσεων SOQL. Επιθεωρητής Σημείου Ελέγχου. Επιθεωρητής κορμού. Χρησιμοποιήστε προσαρμοσμένες προοπτικές στο Log Inspector. Αρχεία εντοπισμού σφαλμάτων
Πώς αποδεικνύετε ισχυρή επαγωγή;

Η αρχή της ισχυρής επαγωγής λέει ότι μπορείτε να αποδείξετε μια δήλωση της μορφής: P(n) για κάθε θετικό ακέραιο n. ως εξής: Βασική περίπτωση: Η P(1) είναι αληθής. Ισχυρό επαγωγικό βήμα: Ας υποθέσουμε ότι το k είναι ένας θετικός ακέραιος έτσι ώστε τα P(1), P(2), P(k) να είναι όλα αληθή. Να αποδείξετε ότι το P(k + 1) είναι αληθές
