
Πίνακας περιεχομένων:
- Συγγραφέας Lynn Donovan donovan@answers-technology.com.
- Public 2023-12-15 23:45.
- Τελευταία τροποποίηση 2025-01-22 17:21.
Κανόνας προσθήκης 2: Όταν δύο γεγονότα, το Α και το Β, είναι δεν αποκλείονται αμοιβαία, υπάρχει κάποια επικάλυψη μεταξύ αυτών των γεγονότων. ο πιθανότητα ότι το Α ή το Β θα συμβεί είναι το άθροισμα απο πιθανότητα κάθε εκδήλωσης, μείον το πιθανότητα της επικάλυψης. P(A ή B) = P(A) + P(B) - P(A και B)
Στη συνέχεια, μπορεί επίσης να ρωτήσει κανείς, ποιος είναι ο κανόνας και στην πιθανότητα;
Κανόνας (για AND): n(A και B) σημαίνει τον αριθμό των αποτελεσμάτων τόσο στο A όσο και στο B. n(S) σημαίνει τον συνολικό αριθμό των πιθανών αποτελεσμάτων (ο χώρος του δείγματος). Ένα ζάρι ρίχνεται. Τι είναι το πιθανότητα ότι ο αριθμός είναι ζυγός και μικρότερος από 4;
πώς μπορείτε να χρησιμοποιήσετε τον γενικό κανόνα πρόσθεσης για να βρείτε την πιθανότητα εμφάνισης του γεγονότος Α ή Β; Κανόνας του Πρόσθεση ο πιθανότητα ότι Εκδήλωση Α ή Γεγονός Β συμβαίνει ισούται με το πιθανότητα ότι Εκδήλωση Α εμφανίζεται συν το πιθανότητα ότι Γεγονός Β συμβαίνει μείον το πιθανότητα ότι και τα δύο Εκδηλώσεις Α και σι συμβούν. P(A ∪ σι ) = P(A) + P( σι ) - Ρ(Α ∩ σι ) Ένας μαθητής πηγαίνει στη βιβλιοθήκη.
Σε σχέση με αυτό, ποιοι είναι οι 3 κανόνες πιθανότητας;
Υπάρχουν τρία βασικός κανόνες σχετίζεται με πιθανότητα : η πρόσθεση, ο πολλαπλασιασμός και το συμπλήρωμα κανόνες . Η προσθήκη κανόνας χρησιμοποιείται για τον υπολογισμό του πιθανότητα του συμβάντος Α ή του γεγονότος Β που συμβαίνει· το εκφράζουμε ως: P(A ή B)
Ποιοι είναι οι 5 κανόνες πιθανοτήτων;
Βασικοί κανόνες πιθανοτήτων
- Κανόνας Πιθανοτήτων 1 (Για οποιοδήποτε συμβάν A, 0 ≤ P(A) ≤ 1)
- Κανόνας πιθανότητας δύο (Το άθροισμα των πιθανοτήτων όλων των πιθανών αποτελεσμάτων είναι 1)
- Τρίτος κανόνας πιθανοτήτων (ο κανόνας του συμπληρώματος)
- Πιθανότητες που περιλαμβάνουν πολλαπλά συμβάντα.
- Κανόνας πιθανοτήτων τέταρτος (κανόνας προσθήκης για ασύνδετα συμβάντα)
- Εύρεση P(A και B) χρησιμοποιώντας τη λογική.
Συνιστάται:
Να κάνετε και να μην κάνετε για την αίθουσα συνεδριάσεων;

Εθιμοτυπία στις επαγγελματικές συναντήσεις: Πρέπει και δεν πρέπει να είστε ακριβείς. Βεβαιωθείτε ότι είστε σε θέση να παρακολουθήσετε τη συνάντηση εγκαίρως. Μην παρουσιάζεστε με το όνομα ή το επίθετό σας. Να είναι προσεκτικός. Μην χρησιμοποιείτε το smartphone σας. Προσπαθήστε να συνεισφέρετε. Να είναι σίγουροι. Βρείτε μια άνετη θέση καθίσματος. Μην τρώτε κατά τη διάρκεια της συνάντησης
Πώς μπορώ να δημιουργήσω έναν κανόνα μεταφοράς στο Office 365;
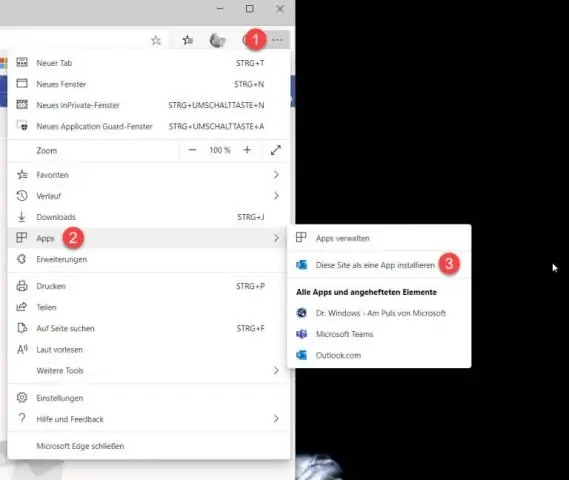
Δημιουργήστε έναν κανόνα μεταφοράς του Office 365 για να τροποποιήσετε το θέμα των μηνυμάτων ώστε να είναι αναγνωρίσιμο. Συνδεθείτε στην πύλη διαχειριστή του Office 365 και μεταβείτε στοExchangeadministration. Μεταβείτε στην ενότητα "Ροή αλληλογραφίας". Κάντε κλικ στο κουμπί προσθήκης και επιλέξτε την επιλογή δημιουργίας νέου κανόνα. Θα εμφανιστεί το νέο παράθυρο κανόνων μεταφοράς
Πώς εξηγείτε την πιθανότητα στους μαθητές;
Η πιθανότητα εκφράζεται συνήθως ως αναλογία του αριθμού των πιθανών αποτελεσμάτων σε σύγκριση με τον συνολικό αριθμό των πιθανών αποτελεσμάτων. Ρωτήστε τους μαθητές αν μπορούν να δώσουν ένα παράδειγμα πιθανοτήτων. Για να βοηθήσετε τους μαθητές να κατανοήσουν τις πιθανότητες, δουλέψτε το ακόλουθο πρόβλημα ως τάξη: Φανταστείτε ότι έχετε επιβιβαστεί σε αεροπλάνο
Πώς υπολογίζετε την υπό όρους πιθανότητα;

Ο τύπος για την υπό όρους πιθανότητα προέρχεται από τον κανόνα πολλαπλασιασμού πιθανοτήτων, P(A και B) = P(A)*P(B|A). Μπορείτε επίσης να δείτε αυτόν τον κανόνα ως P(A∪B). Το σύμβολο της Ένωσης (∪) σημαίνει «και», όπως συμβαίνει στο γεγονός Α και στο γεγονός Β που συμβαίνει
Πώς δημιουργείτε έναν κανόνα NAT στο FortiGate;

Πώς να δημιουργήσετε έναν κανόνα εξερχόμενου στατικού NAT: Μεταβείτε στο: Πολιτική & αντικείμενα > Αντικείμενα > Ομάδες IP. Κάντε κλικ στο κουμπί «Δημιουργία νέου». Όνομα = Ό,τι θέλεις, κάτι περιγραφικό. Σχόλια = Προαιρετικά. Τύπος = Επιλέξτε "One-to-One" Εξωτερικό εύρος IP = Εισαγάγετε απλώς μία δημόσια διεύθυνση IP. Απάντηση ARP = Αποεπιλέξτε αυτό (η προεπιλογή είναι επιλεγμένη)
